Textbooks on economic analysis define a formula to calculate the equivalent future value F of a series of uniform payments A for n periods at interest rate i. It is assumed that the payments occur at the end of each period. Rent, insurance payments or deposits into a savings account occur are beginning-of-period cash flows. What formula should we use in these cases to calculate the equivalent future value?
We need to derive it. We start from an example cash flow:
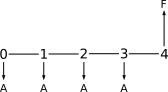
Four uniform payments A are done at the beginning of 4 periods. The equivalent future value F of all the payments is calculated as the sum of the future value of each payment, using the formula F = A(1 + i)n:
F = A(1 + i)4 + A(1 + i)3 + A(1 + i)2 + A(1 + i)
The general case for n years is:
F = A(1 + i)n + A(1 + i)n-1 … + A(1 + i)2 + A(1 + i) (1)
We multiply each side by (1 + i) to obtain:
F(1 + i) = A(1 + i)n+1 + A(1 + i)n … + A(1 + i)2 (2)
We subtract (1) from (2):
Fi = A(1 + i)n+1 - A(1 + i)
Solving for F:
F = A [ (1 + i)n+1 - (1 + i) ]/ i
We now have the general formula for beginning-of-period uniform series future value.
The idea of deriving the formula from a cash flow. came from the book Engineering Economic Analysis by Donald Newman, Ted Eschenbach and Jerome Lavelle, Ninth Edition, 2004, Chapter 4 More interest Formulas, section Uniform Series Compoung Interest Formulas, page 86.