Infinite ladder of resistors
What is the equivalent resistance of an infinite ladder of resistors?
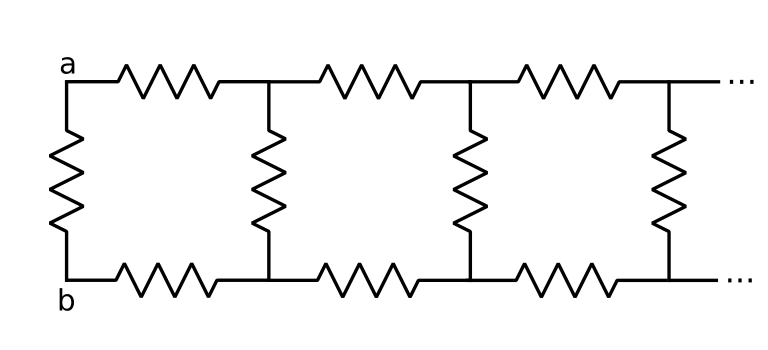
Given the above infinite array of resistors, all of the same value, what is the equivalent resistance between the nodes a and b?
The array can be viewed as a sequence of identical elements, each element having three resistors:
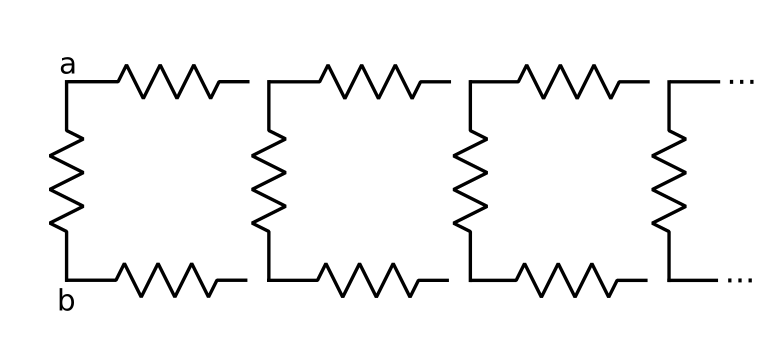
An approach to obtain the equivalent resistance between nodes a and b is to start in the first element, converting resistor R1 in parallel with R2, R3 and the equivalent resistance of the second element in series. The equivalent resistance of the second element is the result of its first resistor in parallel with its two other resistors and the equivalent resistance of the third element. And so for an infinite number of elements.
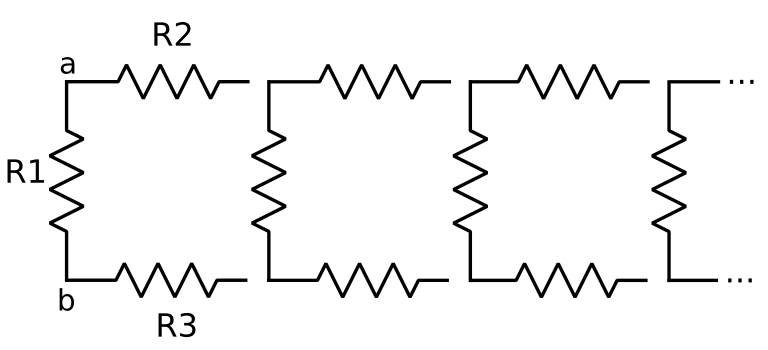
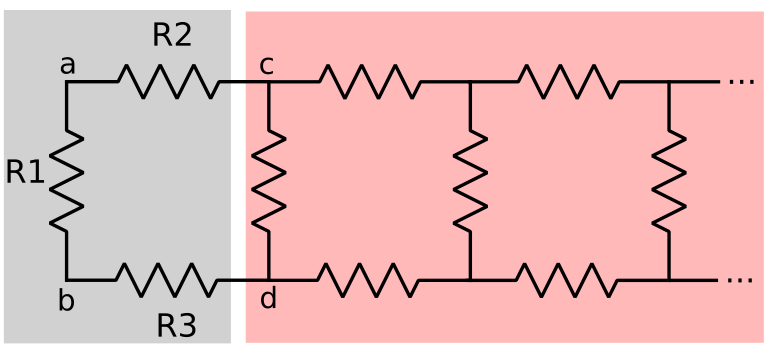
Because of this, a different approach is used. We first separate the array in two networks:
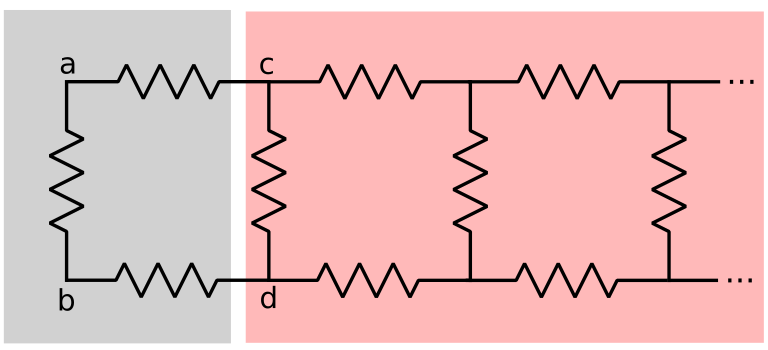
The network on the left is the first element, and the network on the right are the remaining elements, which are infinite and the same as the original infinite array of resistors.
The equivalent resistance between the nodes a and b consists of the resistor R1 in parallel with R2, R3 and the equivalent resistance of the network on the right side in series:
This replaces the whole network as Req:
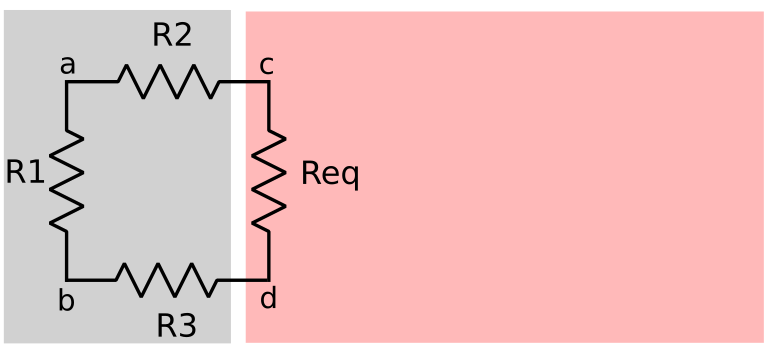
Now the expression to calculate Req between a and b is:
$$ Req = \cfrac{1}{\cfrac{1}{R1} + \cfrac{1}{R2 + Req + R3}} $$
Since all resistance values are equal:
$$ Req = \cfrac{1}{\cfrac{1}{R} + \cfrac{1}{2 R + Req}} $$
Separating Req:
$$ Req^2 + 2 Req - 2R^2 = 0 $$
Solve by using the general quadratic formula:
$$ Req = \cfrac{-2R \pm \sqrt{4R^2 + 4 \cdot 2R^2}}{2} $$
$$ Req = -R \pm \cfrac{\sqrt{4 \cdot 3 R^2}}{2} $$
$$ Req = R(-1 \pm \sqrt{3}) $$
$$ Req = ( \sqrt{3} - 1)R $$
$$ Req = 0.73205080 R $$